[ 통계, 혼돈과 질서의 만남 ]
제 1장 불확실성, 무작위, 그리고 새로운 지식의 창조
<부록 : 토론>
A.1 우연성Chance과 혼돈이론Chaos
제1장의 내용을 토대로 하여 강의를 끝낸 후 진행된 토론시간에는, “무작위 같은Random like” 현상을 기술하는데 사용된 혼돈과, 그것이 우연성 및 불확실성의 연구와 어떤 관련이 있는지에 관하여 질문이 있었습니다. 나는 다음과 같이 대답하였습니다.
우연성Chance이라는 단어는 추첨에서 번호를 뽑아내는 것과 같은 무작위 현상을 기술하기 위하여 사용됩니다. 이렇게 하여 만들어진 일련의 숫자들이 종국에는 어떤 질서를 나타내는데, 이는 확률로 설명할 수 있습니다. 다른 한편, 결정론적 절차에 의하여 생산되는 숫자들은 전체적으로는 규칙을 지니고 있지만 부분적으로는 무작위식 행동을 보일 수 있다는 사실입니다.
지난 20년 동안 과학자들은 혼돈이라는 이름 하에 후자의 현상을 연구했습니다. 이 새로운 접근방식은 구름의 형성, 난류, 해안선과 같은 복잡한 모양이나 형태를 모형화 하는데 사용되었으며, 간단한 수학 방정식들을 사용하여 주식시장의 주가변동을 설명하는데도 이용되었습니다. 이러한 사고방식은 우연성 메커니즘을 통해 어떤 시스템의 결과를 기술하는 것과는 차이가 있습니다.
우연성은 무질서 속의 질서를 다루지만 혼돈이론은 질서 속의 무질서를 다룹니다. 이 둘은 관찰된 현상들을 모형화 한다는 점에서 서로 관계가 있습니다.
로렌츠Edward Lorenz는 시스템의 반응이 초기조건에 민감하다는, 소위 “나비효과”를 발견했는데, 이 발견과 함께 혼돈에 관한 연구가 빛을 발하게 되었습니다. 그는 장기 일기예측시, 예측공식에 입력으로 사용되는 초기 측정치의 작은 오류가 결과적으로 예측 값에 매우 큰 오류를 발생시킨다는 것을 발견하였습니다.
맨델브롯Benoit Mandelbrot은 각각 다른 규모 들에서 같은 종류의 변화를 보이는 형태들의 모양을 설명하기 위하여 프랙탈 기하학을 만들어 냈 습니다. 그의 프랙탈 기하학을 이용하면 눈송이나 해안선의 구조와 같이 자연 속에서 발견될 수 있는 “들쭉날쭉하고, 엉클어지고, 쪼개지고, 비틀어지고, 부서진” 모양들을 설명할 수가 있습니다. 파이겐바움Mitchell J. Feigenbaum은 아래와 같은 반복함수에 기초하여 매력적 개념을 만들어 냈습니다.
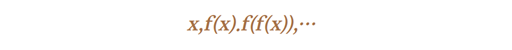
이것은 불안정한 난류와 같은 몇 가지 물리적 현상에 대하여 정확한 모델을 제공합니다. 과학자들이 말하는 혼돈이론은 사실 수학적인 것이며 이에 대한 연구는 컴퓨터를 이용함으로써 가능 해졌고 그 결과 그것은 매력적인 것이 되었습니다. 이제 그것은 충분히 보람 있는 연구분야가 되었으며 또한 결정론적 모형들을 통하여 자연 속에서 관찰되는 현상들을 모형화 하는 새로운 방법을 개척하였습니다.
유명한 수학자인 칵Mark Kac은 결정론적 함수의 그래프가 어떻게 무작위 메커니즘의 기록과 유사해지는가를 나타내는 흥미로운 예를 제시했습니다(그의 자서전 “우연성의 수수께끼Enigmas of Chance”, pp. 74-76 참조). 스몰 루쵸우스키Smoluchowski의 이론인 브라운 운동, 즉 공기를 담은 용기 속에 석영섬유에 매달린 작은 거울의 움직임을 실험하기 위하여 캐플러Kappler는 1931년에 교묘한 실험으로 거울의 움직임을 나타낸 정밀한 기록을 얻었습니다. 다음의 그림은 그중 30초간의 기록입니다.
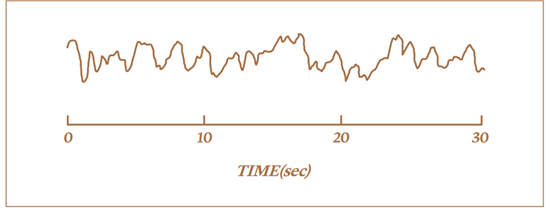
칵은 이 그래프를 보면서 다음과 같은 말을 했습니다. “사람은 늘 우연성에 부딪치게 되며 이 기록은 오직 무작위 메커니즘에 의해서만이 가능했을 것이라는 느낌을 지울 수 없습니다.” 캐플러의 실험은 공기분자가 거울에 무작위로 부딪쳐서 그 거울의 움직이는 그래프가 정상 가우스과정을 나타낸다는, 스몰 루쵸우스키의 이론을 확인시켜준 것으로 볼 수 있습니다.
칵은 아래의 함수를 만들어서 그래프를 그려본 결과 캐플러의 그래프와 거의 유사한 형태가 만들어진다는 것을 증명했습니다. 그 어떤 통계적 분석으로도 칵의 함수에 의한 그래프와 캐플러의 그래프 사이의 차이점을 분별할 수 없습니다.
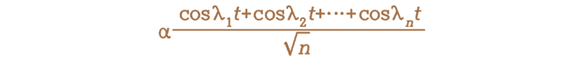
위 함수에서 n은 충분히 큰 수Sufficiently large n를 나타내며, λ1, λ2,…, λn 은 일련의 상수, α는 척도인자입니다. 칵은 질문합니다.