[ 통계, 혼돈과 질서의 만남 ]
2. 무작위와 난수
2.1 난수에 관한 책!(2)
<표1.1>은 흰 구슬(W)과 검은 구슬(B)이 같은 수만큼 들어간 주머니에서 복원하면서 1,000개의 구슬을 꺼냈을 때 색깔의 배열을 나타낸 것입니다. <표1.2>는 병원에서 출생한 1,000명의 어린아이의 성(남성은 M, 여성은 F)을 순서대로 배열한 것입니다.
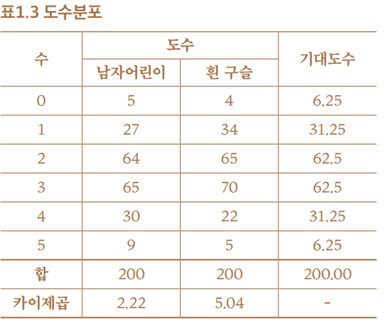
<표1.1>과 <표1.2>를 도수분포의 형태로 요약할 수 있습니다. <표1.3>은 연속적으로 태어난 5명의 아이를 1조로 하여 이 가운데 남아의 수(0~5)에 대한 도수와, 연속적으로 추출된 5개의 구슬을 1조로 하여 이 가운데 흰 공의 수(0~5)에 대한 도수를 함께 나타낸 표입니다.
기대도수란 이론적인 값으로서, 200회의 실험을 무수히 많이 반복했을 때 평균적으로 얻어지는 값을 말합니다. 도수는 히스토그램의 형태로 표현할 수 있습니다.
이 두 종류의 히스토그램이 비슷하다는 것은 아이들의 성을 결정하는 확률 메커니즘이 같은 수의 두 종류(검은 색과 흰 색) 구슬이 들어있는 바구니에서 흰 구슬이나 검은 구슬을 꺼내는 메커니즘, 또는 동전을 던져서 앞면과 뒷면을 결정하는 메커니즘과 유사하다는 점을 시사하고 있습니다.
위에서와 같은 간단한 실습이 성性결정의 이론을 형성하는데 있어 기초를 제공할 수 있다는 것입니다. 신은 동전을 던지고 있는 것입니다! 사실 통계적 검정결과는 남녀 출생표에서 얻어진 이진수가 인위적으로 얻어진 이진수보다도 더욱 신뢰할 수 있는 무작위 수열이라는 것을 보여주었습니다. 아마도 신은 보다 완벽한 동전을 던지고 있는가 봅니다. 인도에서는 일초에 1명 꼴로 아이가 출생하는데, 이는 이진 난수열을 만들기 위한 값싸고도 신속한 자료가 됩니다.


실제로 컴퓨터 이외에 이극관Reverse-biased diode과 같은 자연적인 고안장치들이 난수를 만들기 위하여 사용되는데, 이는 원자수준에서 일정한 이벤트들의 무작위성을 가정하는 양자역학의 이론에 기반을 두고 있습니다. 이 이론 자체가 이렇게 관측된 숫자들을 인위적으로 고안된 장치로 얻어진 수열과 비교함으로써 증명될 수 있다는 사실에 주목하십시오.
그러나 수학자들은 많은 기준들을 만족하는 적절한 난수열을 만들기 위해서는 무작위 절차가 아닌 적절한 결정론적 절차를 취해야 한다고 믿고 있습니다!(이 주제에 관한 훌륭한 토론이 헐과 도벨Hull and Dobell(1962)의 논문에 있습니다.) 이렇게 만들어진 숫자들은 유사난수Pseudo-random라고 부르는데, 실제 응용분야에서 널리 이용되고 있습니다.
우리는 이미 인위적으로 생성된 일련의 난수들이 자연적으로 생성되는 일련의 난수들과 유사한 확률 메커니즘을 가지고 있다는 사실을 살펴보았으며, 아울러 남녀 출생과 같은 자연적 사건들의 발생을 설명하고 있다는 사실도 살펴보았습니다. 우리를 당황케 하는 어려운 문제들이나 정확한 해답을 구하기에는 너무도 복잡한 문제들을 풀기 위하여, 새로운 정보를 만들어 내기 위하여, 또는 새로운 아이디어를 얻기 위하여 여러가지 방법으로 무작위를 이용할 수 있습니다. 이중 몇 가지를 간략히 기술하고자 합니다.