²¹ 2. 불확실성 길들이기

[ 통계, 혼돈과 질서의 만남 ]

제가 이미 언급한 것처럼 원래 통계학의 어원학적 의미는 자료를 수집하여 분류하는 행위 및 이를 정책수립과정에 이용하는 것입니다.

19세기 들어서 통계학은 새로운 의미를 갖기 시작했는데 그것은 자료의 해석 및 의사결정을 위한 정보의 추출입니다. 현재의 경향을 근거로 인구의 사회경제적 특성을 어떻게 예측할 수 있을까요? 정부에서 채택한 법률의 효과는 어떻게 나타날까요? 사회복지를 증진시키기 위해서는 정책결정을 어떻게 해야 할까요? 흉작을 막고 죽음과 재해를 줄이기 위한 시스템을 개발할 수 있을까요?

여기에 만족스러운 답을 원하는 또 다른 질문들이 있습니다. 내일 비가 올까요? 현재의 따듯한 기후가 얼마나 지속될까요? 과학적 수준에서 관측자료가 주어진 이론에 잘 부합할까요? 개인적인 차원에서는 다음과 같은 형태의 질문이 제기될 수 있습니다. 내가 선택한 직업에 대해서 어떤 전망을 가질 수 있을까요? 수익을 극대화하려면 어떻게 투자해야 할까요?

이러한 유형의 질문에 대한 해를 찾는데 있어서 가장 방해가 되는 것은 불확실성Uncertainty–원인과 결과사이의 1:1 대응관계의 결핍-입니다. 그렇다면 불확실성 하에서 어떻게 해야 할까요? 이러한 문제가 오랫동안 인류를 곤혹스럽게 해왔습니다.

불확실성을 통제하여 의사결정의 과학으로 개발하게 된 것은 단지 20세기 초입니다. 일상생활에서 우리를 당혹스럽게 하는 이러한 문제들에 대해, 그 해답을 찾는데 이처럼 오랜 시간이 걸린 이유는 무엇일까요? 이 질문에 답하기 위해, 문제를 해결하고자 할 때나 새로운 지식을 창출하고자 할 때 적용하는 논리과정 또는 추론 형태에 대해 알아보고, 지난 20세기 동안 변화한 우리의 사유구조변화에 대해 생각해 보겠습니다.

2.1 논리적 추론의 세 가지 유형

2.1.1 연역법Deduction

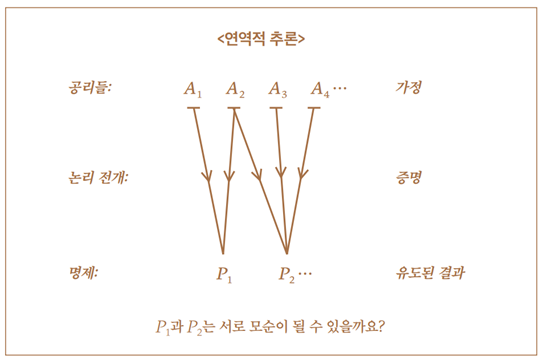
연역적 추론은 2000년 전 그리스의 철학자들에 의해 소개되었으며 지난 수세 기에 걸쳐 수학의 연구를 통해 완성되었습니다. 그 자체가 참인 전제Premises 또는 공리Axioms가 A1, A2, A3, …로 주어졌다고 합시다. 우리는 이 공리들 중 일부, 예를 들면 A1, A2를 이용하여 명제Proposition P1을 증명할 수 있습니다. 명제 P1이 참인가는 전적으로 공리 A1, A2가 참인가에 달려 있습니다. 이 논리 전개과정에서 다른 공리들을 명시적으로 사용하지 않은 사실은 아무런 문제가 되지 않습니다. 마찬가지로 공리 A2, A3, A4를 사용하여 명제 P2를 유도할 수도 있습니다.

연역적 추론에서는 전제이상의 어떠한 새로운 지식도 얻을 수 없습니다. 왜냐하면 유도된 모든 명제들은 공리들 속에 함축되어 있기 때문입니다. 공리들이나 이로부터 유도된 명제들은 현실과는 동떨어져 있는데 다음의 인용문들이 이를 특징적으로 보여줍니다.

수학의 기본이 되는 연역적 논리가 “최고의 선”으로 생각되는 것은 논리적 결함이 없을 수 없습니다. 앞에서 보았듯이, 연역적 논리에서는 하나의 명제를 증명하기 위해 공리들의 일부를 사용하고 나머지 공리들을 사용하지 않는 것은 아무런 문제가 되지 않습니다.

그러면 다음과 같은 질문이 제기됩니다. 공리들의 부분집합A1, A2가 명제 P를 함축하고, 다른 부분집합 A2, A3, A4는 P를 부정하는 명제를 함축하는 경우가 가능할까요? 예를 들어, 가정 A1, A2 는 삼각형의 내각의 합이 180도가 되는 것을 함축하고, 가정 A2, A3, A4는 180도가 아닌 다른 값을 함축하는 것이 가능할까요?

수학의 공리들에서는 이러한 모순이 생길 수 없다는 것을 증명하기 위한 많은 시도들이 있었는데, 이 시도들은 결국 놀라운 결과들을 가져왔습니다. 유명한 수학논리학자인 괴델Godel은 정교한 논술로 매우 교묘한 증명을 세상에 제시하였습니다. 그에 의하면 일정한 공리들A given set of axioms을 근거로 하여 추론할 경우, 이 방식이 모순으로 귀결될 수 있다는 가능성에 대해 반증할 수 없다는 것입니다.

또한 만약 일단의 공리들A system of axioms이 명제 P뿐만 아니라 P의 부정 명제를 허용한다면, 이 같은 일단의 공리들로부터 우리가 원하는 어떠한 모순도 유도될 수 있다는 것이 입증되었습니다. 센테니얼리뷰지The Centennial Review 1958년 11호에 게재된 로날드 피셔Ronald Fisher 경의 기고문 “확률의 특성Nature of Probability”에서 한 일화를 인용하고자 합니다.

수학은 엄격한 규칙으로 하는 게임이지만 어느 날 모순된 문제들이 무더기로 발견될지는 아무도 모릅니다